In mathematics the problem of trisecting an angle is a very interesting one. Perhaps more so, due to its seemingly impossible nature when compared to the similar problem of bisection of an angle which is easily achieved using compass and straightedge. Several literature have shown the problem to be impossible to solve using Euclidian geometric construction tools. However the problem is not impossible in nature. I have got a brilliant way of doing this using a very old technique originally attributed to Archimedes, the famous Greek mathematician.
The construction does not follow the Euclidean rules of construction which were used to prove its impossibility. However there is a bit out confusion about the rules themselves, as they are nowhere clearly mentioned in the writings of Euclid. However, most of the scholars agree on a set of rules apparent from the constructions described by Euclid. The following construction circumvents the rules, but does manage to trisect an angle accurately.
Archimedes’s method of Trisection of Angle
Let the angle to be trisected be AOB as shown in the figure. The trisected angle is PRA where 3xPRA = AOB (will be proved).
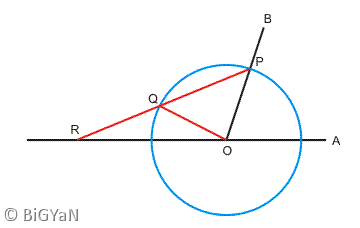
The steps of construction:
-
Using compass draw a circle with O as center. The intersection of the circle with OB is marked as P.
-
Draw like PR intersecting the circle at Q, such that QR = OP, where the point R is collinear with O and A. This is achieved by marking the distance OP on the straightedge and aligning the markings with the like OA extended backwards. Although it may seem a difficult procedure, it is actually quite easy to do.
-
Angle PRO is the trisected angle of AOB
Proof of Correctness
The proof is quite easy. I have put it down in a step by step way:
-
OP = OQ, as P and Q are points on circumference and O is the center of the circle.
-
triangle_POQ is isosceles, so angle_PQO = angle_QPO
-
angle_QOP + angle_PQO + angle_QPO = 180
=> angle_QOP = 180 – 2*angle_QPO -
angle_RQO = 180 – angle_PQO = 180 – angle_QPO
-
triangle_RQO is also isosceles as QR = OP = QO, so angle_QOR = angle_QRO
-
angle_RQO + angle_QRO + angle_QOR = 180
=> 180 – angle_QPO + angle_QRO + angle_QOR = 180
=> angle_QRO + angle_QOR = angle_QPO
=> angle_QPO = 2*angle_QRO -
angle_AOB + angle_POR = 180
=> angle_AOB + angle_QOP + angle_QOR = 180
=> angle_AOB + (180 – 2*angle_QPO) + angle_QRO = 180
=> angle_AOB – 2*angle_QPO + angle_QRO = 0
=> angle_AOB – 2*(2*angle_QRO) + angle_QRO = 0
=> 3*angle_QRO = angle_AOB
=> angle_QRO = (1/3) * angle_AOB -
Hence we conclude that angle_QRO is the trisection of angle_AOB
So what is the catch?
There is no catch, the proof is indeed correct. In the beginning I have mentioned that the problem is impossible in nature, yet the proof that we showed is correct. The problem lies with the point 2 of the construction. The step required us to do a marking on the straightedge, which is not permissible in Euclidean constructions.
Bending the Rules !!
So you can actually intersect an angle after all, using the standard set of tools only. But the construction is not Euclidian. The interesting part is that this construction is quite old, but somehow this did not receive much publicity as the problem itself. Sometimes to solve a problem you have to bend the rules a bit.
There is a catch. Neusis can only "solve" the problem at the resolution of what your eye can see. You cannot converge 2 distances exactly. Greater magnification will show that neusis is not correct. That's why it never caught on. It has nothing to do with whether a ruler is marked or not.
ReplyDeletehttp://www.flickr.com/photos/85937466@N02/10099206904/in/set-72157636438514124
There is a catch. Neusis can only "solve" the problem at the resolution of what your eye can see. You cannot converge 2 distances exactly. Greater magnification will show that neusis is not correct. That's why it never caught on. It has nothing to do with whether a ruler is marked or not.
ReplyDeletehttp://www.flickr.com/photos/85937466@N02/10099206904/in/set-72157636438514124